An array is a systematic arrangement of objects, usually in rows and columns. Specifically, it may refer to several things.
An array is a systematic arrangement of objects, usually in rows and columns. Specifically, it may refer to several things.
In computer science
Generally, a collection of data items that can be selected by indices computed at run-time, including:
* Array data structure, an arrangement of items at equally spaced addresses in computer memory
* Array data type, used in a programming language to specify a variable that can be indexed
* Associative array, an abstract data structure model that generalizes arrays to arbitrary indices
or various kinds of the above, such as
* Bit array or bit vector
* Dynamic array, allocated at run time
* Parallel array of records, with each field stored as a separate array
* Sparse array, with most elements omitted, to store a sparse matrix
* Variable-length array
* Ragged (jagged) array, where the rows have different lengths individually
or various related concepts:
* Array processor, a computer to process arrays of data (not to be confused with a processor array)
* Array programming, using matrix algebra notation in programs (not the same as array processing)
* Array slicing, the extraction of sub-arrays of an array
* APL (programming language)
or also:
* Video Graphics Array (VGA), a display adapter and video format, and many variants thereof (EVGA, FWVGA, QVGA, QXGA, SVGA, SXGA, SXGA+, TXGA, UVGA, XGA, XGA+, ...)
In computer science, an array data structure or simply array is a data structure consisting of a collection of elements (values or variables), each identified by one or more integer indices, stored so that the address of each element can be computed from its index tuple by a simple mathematical formula.
For example, an array of 10 integer variables, with indices 0 through 9, may be stored as 10 words at memory addresses 2000, 2004, 2008, … 2036; so that the element with index i has address 2000 + 4 × i.
One-dimensional arrays
The one dimensional arrays are also known as Single dimension array and is a type of Linear Array. In the one dimension array the data type is followed by the variable name which is further followed by the single subscript i.e. the array can be represented in the row or column wise. It contains a single subscript that is why it is known as one dimensional array because one subscript can either represent a row or a column.
for example auto int new[10];
In the given example the array starts with auto storage class and is of integer type named new which can contain 10 elements in it i.e. 0-9. It is not necessary to declare the storage class as the compiler initializes auto storage class by default to every data type After that the data type is declared which is followed by the name i.e. new which can contain 10 entities.
For a vector with linear addressing, the element with index i is located at the address B + c · i, where B is a fixed base address and c a fixed constant, sometimes called the address increment or stride.
If the valid element indices begin at 0, the constant B is simply the address of the first element of the array. For this reason, the C programming language specifies that array indices always begin at 0; and many programmers will call that element "zeroth" rather than "first".
However, one can choose the index of the first element by an appropriate choice of the base address B. For example, if the array has five elements, indexed 1 through 5, and the base address B is replaced by B − 30c, then the indices of those same elements will be 31 to 35. If the numbering does not start at 0, the constant B may not be the address of any element.
Multidimensional arrays
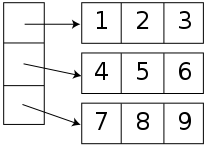
For a two-dimensional array, the element with indices i,j would have address B + c · i + d · j, where the coefficients c and d are the row and column address increments, respectively.
More generally, in a k-dimensional array, the address of an element with indices i1, i2, …, ik is
B + c1 · i1 + c2 · i2 + … + ck · ik
This formula requires only k multiplications and k−1 additions, for any array that can fit in memory. Moreover, if any coefficient is a fixed power of 2, the multiplication can be replaced by bit shifting.
The coefficients ck must be chosen so that every valid index tuple maps to the address of a distinct element.
If the minimum legal value for every index is 0, then B is the address of the element whose indices are all zero. As in the one-dimensional case, the element indices may be changed by changing the base address B. Thus, if a two-dimensional array has rows and columns indexed from 1 to 10 and 1 to 20, respectively, then replacing B by B + c1 - − 3 c1 will cause them to be renumbered from 0 through 9 and 4 through 23, respectively. Taking advantage of this feature, some languages (like FORTRAN) specify that array indices begin at 1, as in mathematical tradition; while other languages (like Pascal and Algol) let the user choose the minimum value for each index.
In computer science, an array type is a data type that is meant to describe a collection of elements (values or variables), each selected by one or more indices that can be computed at run time by the program. Such a collection is usually called an array variable, array value, or simply array.[1] By analogy with the mathematical concepts of vector and matrix, an array type with one or two indices is often called a vector type or matrix type, respectively.
Language support for array types may include certain built-in array data types, some syntactic constructions (array type constructors) that the programmer may use to define such types and declare array variables, and special notation for indexing array elements.[1] For example, in the Pascal programming language, the declaration type MyTable: array [1..4,1..2] of integer, defines a new array data type called MyTable. The declaration var A: MyTable then defines a variable A of that type, which is an aggregate of eight elements, each being an integer variable identified by two indices. In the Pascal program, those elements are denoted A[1,1], A[1,2], A[2,1],… A[4,2].
Special array types are often defined the language's standard libraries.
Array types are distinguished from record types mainly because they allow the element indices to be computed at run time, as in the Pascal assignment A[I,J] := A[N-I,2*J]. Among other things, this feature allows a single iterative statement to process arbitrarily many elements of an array variable.
In more theoretical contexts, especially in type theory and in the description of abstract algorithms, the terms "array" and "array type" sometimes refer to an abstract data type (ADT) also called abstract array or associative array, a mathematical model with the basic operations and behavior of a typical array type in most languages — basically, a collection of elements that are selected by indices computed at run-time.
Depending on the language, array types may overlap (or be identified with) other data types that describe aggregates of values, such as lists and strings. Array types are often implemented by array data structures, but sometimes by other means, such as hash tables, linked lists, or search trees.
In order to effectively implement variables of such types as array structures (with indexing done by pointer arithmetic), many languages restrict the indices to integer data types (or other types that can be interpreted as integers, such as bytes and enumerated types), and require that all elements have the same data type and storage size. Most of those languages also restrict each index to a finite interval of integers, that remains fixed throughout the lifetime of the array variable. In some compiled languages, in fact, the index ranges may have to be known at compile time.
On the other hand, some programming languages provide more liberal array types, that allow indexing by arbitrary values, such as floating-pont numbers, strings, objects, references, etc.. Such index values cannot be restricted to an interval, much less a fixed interval. So, these languages usually allow arbtrary new elements to be created at any time. This choice precludes the implementation of array types as array data strcutures. That is, those languages use array-like syntax to implement a more general associative array semantics, and must therefore be implemented by a hash table or some other search data structure.
The number of indices needed to specify an element is called the dimension, dimensionality, or rank of the array type. (This nomenclature conflicts with the concept of dimension in linear algebra, where it is the number of elements. Thus, an array of numbers with 5 rows and 4 columns (hence 20 elements) is said to have dimension 2 in computing contexts, but 20 in mathematics. Also, the computer science meaning of "rank" is similar to its meaning in tensor algebra but not to the linear algebra concept of rank of a matrix.)
Many languages support only one-dimensional arrays. In those languages, a multi-dimensional array is typically represented by an Iliffe vector, a one-dimensional array of references to arrays of one dimension less. A two-dimensional array, in particular, would be implemented as a vector of pointers to its rows. Thus an element in row i and column j of an array A would be accessed by double indexing (A[i][j] in typical notation). This way of emulating multi-dimensional arrays allows the creation of ragged or jagged arrays, where each row may have a different size — or, in general, where the valid range of each index depends on the values of all preceding indices.
This representation for multi-dimensional arrays is quite prevalent in C and C++ software. However, C and C++ will use a linear indexing formula for multi-dimensional arrays that are declared as such, e.g. by int A[10][20] or int A[m][n], instead of the traditional int **A.
Index types
Array data types are most often implemented as array structures: with the indices restricted to integer (or totally ordered) values, index ranges fixed at array creation time, and multilinear element addressing. This was the case in most "third generation" languages, and is still the case of most systems programming languages such as Ada, C, and C++. In some languages, however, array data types have the semantics of associative arrays, with indices of arbitrary type and dynamic element creation. This is the case in some scripting languages such as Awk and Lua, and of some array types provided by standard C++ libraries.
Array index range queries
Some programming languages provide operations that return the size (number of elements) of a vector, or, more generally, range of each index of an array. In C and C++ arrays. They do not support the size function, so programmers often have to declare separate variable to hold the size, and pass it to procedures as a separate parameter.
Elements of a newly created array may have undefined values (as in C), or may be defined to have a specific "default" value such as 0 or a null pointer (as in Java).
In C++ a vector supports the store, select, and append operations with the performance characteristics discussed above. Vectors can be queried for their size and can be resized. Slower operations like inserting an element in the middle are also supported.

No comments:
Post a Comment